Sparse Matrix
What is Sparse Matrix?
In computer programming, a matrix can be defined with a 2-dimensional array. Any array with 'm' columns and 'n' rows represent a m X n matrix. There may be a situation in which a matrix contains more number of ZERO values than NON-ZERO values. Such matrix is known as sparse matrix.
Sparse matrix is a matrix which contains very few non-zero elements.
When a sparse matrix is represented with a 2-dimensional array, we waste a lot of space to represent that matrix. For example, consider a matrix of size 100 X 100 containing only 10 non-zero elements. In this matrix, only 10 spaces are filled with non-zero values and remaining spaces of the matrix are filled with zero. That means, totally we allocate 100 X 100 X 2 = 20000 bytes of space to store this integer matrix. And to access these 10 non-zero elements we have to make scanning for 10000 times. To make it simple we use the following sparse matrix representation.
Sparse Matrix Representations
A sparse matrix can be represented by using TWO representations, those are as follows...
- Triplet Representation (Array Representation)
- Linked Representation
Triplet Representation (Array Representation)
In this representation, we consider only non-zero values along with their row and column index values. In this representation, the 0th row stores the total number of rows, total number of columns and the total number of non-zero values in the sparse matrix.
For example, consider a matrix of size 5 X 6 containing 6 number of non-zero values. This matrix can be represented as shown in the image...
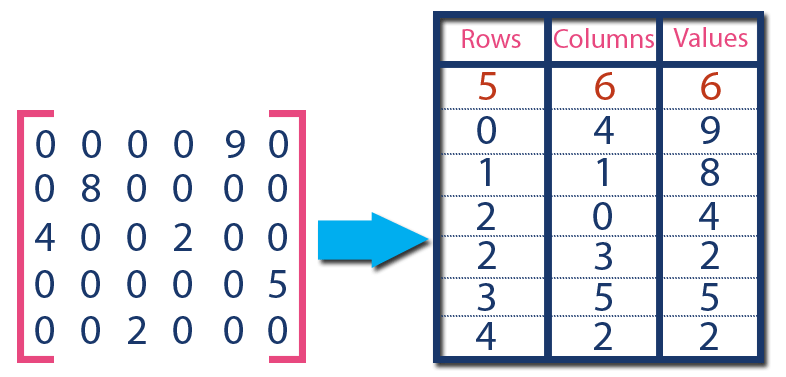
In above example matrix, there are only 6 non-zero elements ( those are 9, 8, 4, 2, 5 & 2) and matrix size is 5 X 6. We represent this matrix as shown in the above image. Here the first row in the right side table is filled with values 5, 6 & 6 which indicates that it is a sparse matrix with 5 rows, 6 columns & 6 non-zero values. The second row is filled with 0, 4, & 9 which indicates the non-zero value 9 is at the 0th-row 4th column in the Sparse matrix. In the same way, the remaining non-zero values also follow a similar pattern.
Implementation of Array Representation of Sparse Matrix using C++
#include<iostream>
using namespace std;
int main()
{
// sparse matrix of class 5x6 with 6 non-zero values
int sparseMatrix[5][6] =
{
{0 , 0 , 0 , 0 , 9, 0 },
{0 , 8 , 0 , 0 , 0, 0 },
{4 , 0 , 0 , 2 , 0, 0 },
{0 , 0 , 0 , 0 , 0, 5 },
{0 , 0 , 2 , 0 , 0, 0 }
};
// Finding total non-zero values in the sparse matrix
int size = 0;
for (int row = 0; row < 5; row++)
for (int column = 0; column < 6; column++)
if (sparseMatrix[row][column] != 0)
size++;
// Defining result Matrix
int resultMatrix[3][size];
// Generating result matrix
int k = 0;
for (int row = 0; row < 5; row++)
for (int column = 0; column < 6; column++)
if (sparseMatrix[row][column] != 0)
{
resultMatrix[0][k] = row;
resultMatrix[1][k] = column;
resultMatrix[2][k] = sparseMatrix[row][column];
k++;
}
// Displaying result matrix
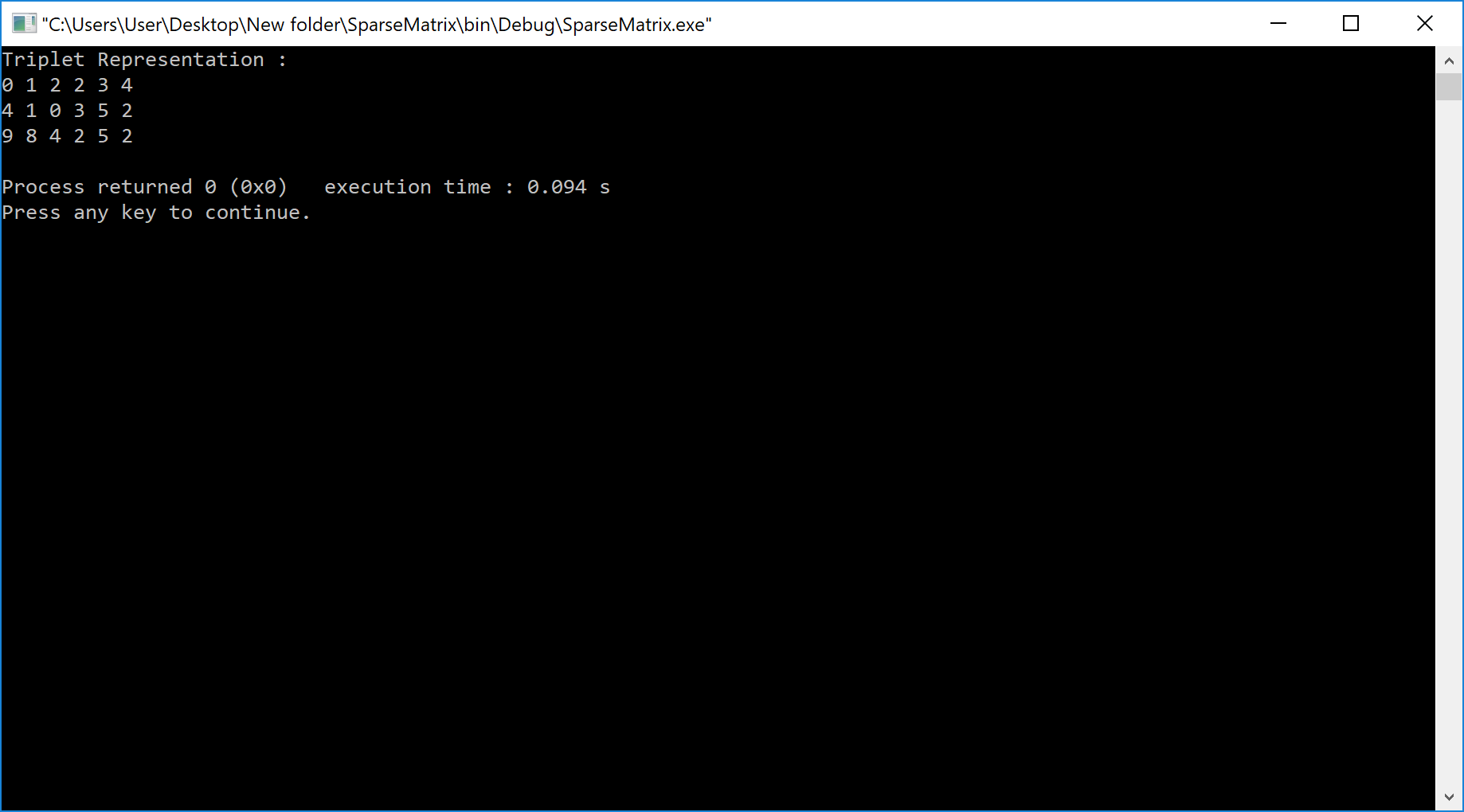
cout<<"Triplet Representation : "<<endl;
for (int row=0; row<3; row++)
{
for (int column = 0; column<size; column++)
cout<<resultMatrix[row][column]<<" ";
cout<<endl;
}
return 0;
}
Output
Linked Representation
In linked representation, we use a linked list data structure to represent a sparse matrix. In this linked list, we use two different nodes namely header node and element node. Header node consists of three fields and element node consists of five fields as shown in the image...

Consider the above same sparse matrix used in the Triplet representation. This sparse matrix can be represented using linked representation as shown in the below image...
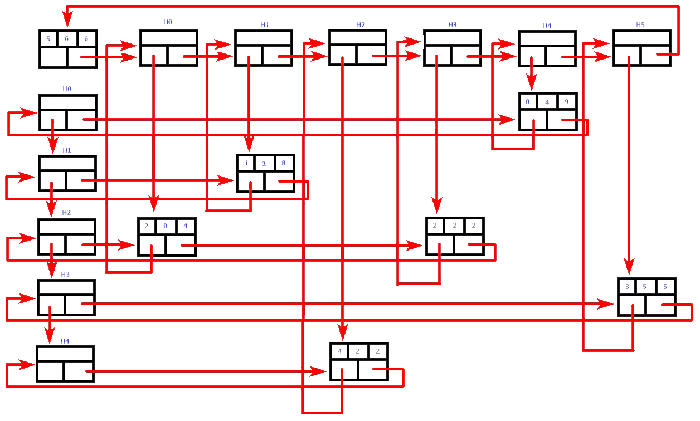
In the above representation, H0, H1,..., H5 indicates the header nodes which are used to represent indexes. Remaining nodes are used to represent non-zero elements in the matrix, except the very first node which is used to represent abstract information of the sparse matrix (i.e., It is a matrix of 5 X 6 with 6 non-zero elements).
In this representation, in each row and column, the last node right field points to its respective header node.
