Binary Tree Traversals
When we wanted to display a binary tree, we need to follow some order in which all the nodes of that binary tree must be displayed. In any binary tree, displaying order of nodes depends on the traversal method.
Displaying (or) visiting order of nodes in a binary tree is called as Binary Tree Traversal.
There are three types of binary tree traversals.
- In - Order Traversal
- Pre - Order Traversal
- Post - Order Traversal
Consider the following binary tree...
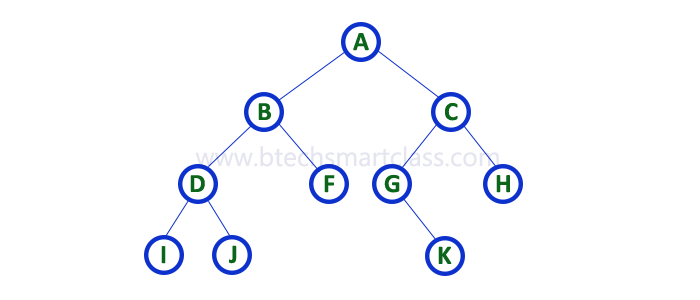
1. In - Order Traversal ( leftChild - root - rightChild )
In In-Order traversal, the root node is visited between the left child and right child. In this traversal, the left child node is visited first, then the root node is visited and later we go for visiting the right child node. This in-order traversal is applicable for every root node of all subtrees in the tree. This is performed recursively for all nodes in the tree.
In the above example of a binary tree, first we try to visit left child of root node 'A', but A's left child 'B' is a root node for left subtree. so we try to visit its (B's) left child 'D' and again D is a root for subtree with nodes D, I and J. So we try to visit its left child 'I' and it is the leftmost child. So first we visit 'I' then go for its root node 'D' and later we visit D's right child 'J'. With this we have completed the left part of node B. Then visit 'B' and next B's right child 'F' is visited. With this we have completed left part of node A. Then visit root node 'A'. With this we have completed left and root parts of node A. Then we go for the right part of the node A. In right of A again there is a subtree with root C. So go for left child of C and again it is a subtree with root G. But G does not have left part so we visit 'G' and then visit G's right child K. With this we have completed the left part of node C. Then visit root node 'C' and next visit C's right child 'H' which is the rightmost child in the tree. So we stop the process.
That means here we have visited in the order of I - D - J - B - F - A - G - K - C - H using In-Order Traversal.
I - D - J - B - F - A - G - K - C - H
2. Pre - Order Traversal ( root - leftChild - rightChild )
In Pre-Order traversal, the root node is visited before the left child and right child nodes. In this traversal, the root node is visited first, then its left child and later its right child. This pre-order traversal is applicable for every root node of all subtrees in the tree.
In the above example of binary tree, first we visit root node 'A' then visit its left child 'B' which is a root for D and F. So we visit B's left child 'D' and again D is a root for I and J. So we visit D's left child 'I' which is the leftmost child. So next we go for visiting D's right child 'J'. With this we have completed root, left and right parts of node D and root, left parts of node B. Next visit B's right child 'F'. With this we have completed root and left parts of node A. So we go for A's right child 'C' which is a root node for G and H. After visiting C, we go for its left child 'G' which is a root for node K. So next we visit left of G, but it does not have left child so we go for G's right child 'K'. With this, we have completed node C's root and left parts. Next visit C's right child 'H' which is the rightmost child in the tree. So we stop the process.
That means here we have visited in the order of A-B-D-I-J-F-C-G-K-H using Pre-Order Traversal.
A - B - D - I - J - F - C - G - K - H
3. Post - Order Traversal ( leftChild - rightChild - root )
In Post-Order traversal, the root node is visited after left child and right child. In this traversal, left child node is visited first, then its right child and then its root node. This is recursively performed until the right most node is visited.
Here we have visited in the order of I - J - D - F - B - K - G - H - C - A using Post-Order Traversal.
I - J - D - F - B - K - G - H - C - A
Program to Create Binary Tree and display using In-Order Traversal - C Programming
#include<stdio.h>
#include<conio.h>
struct Node{
int data;
struct Node *left;
struct Node *right;
};
struct Node *root = NULL;
int count = 0;
struct Node* insert(struct Node*, int);
void display(struct Node*);
void main(){
int choice, value;
clrscr();
printf("\n----- Binary Tree -----\n");
while(1){
printf("\n***** MENU *****\n");
printf("1. Insert\n2. Display\n3. Exit");
printf("\nEnter your choice: ");
scanf("%d",&choice);
switch(choice){
case 1: printf("\nEnter the value to be insert: ");
scanf("%d", &value);
root = insert(root,value);
break;
case 2: display(root); break;
case 3: exit(0);
default: printf("\nPlease select correct operations!!!\n");
}
}
}
struct Node* insert(struct Node *root,int value){
struct Node *newNode;
newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->data = value;
if(root == NULL){
newNode->left = newNode->right = NULL;
root = newNode;
count++;
}
else{
if(count%2 != 0)
root->left = insert(root->left,value);
else
root->right = insert(root->right,value);
}
return root;
}
// display is performed by using Inorder Traversal
void display(struct Node *root)
{
if(root != NULL){
display(root->left);
printf("%d\t",root->data);
display(root->right);
}
}
Output
