Radix sort is one of the sorting algorithms used to sort a list of integer numbers in order. In radix sort algorithm, a list of integer numbers will be sorted based on the digits of individual numbers. Sorting is performed from least significant digit to the most significant digit.
Radix sort algorithm requires the number of passes which are equal to the number of digits present in the largest number among the list of numbers. For example, if the largest number is a 3 digit number then that list is sorted with 3 passes.

Step by Step Process

The Radix sort algorithm is performed using the following steps...

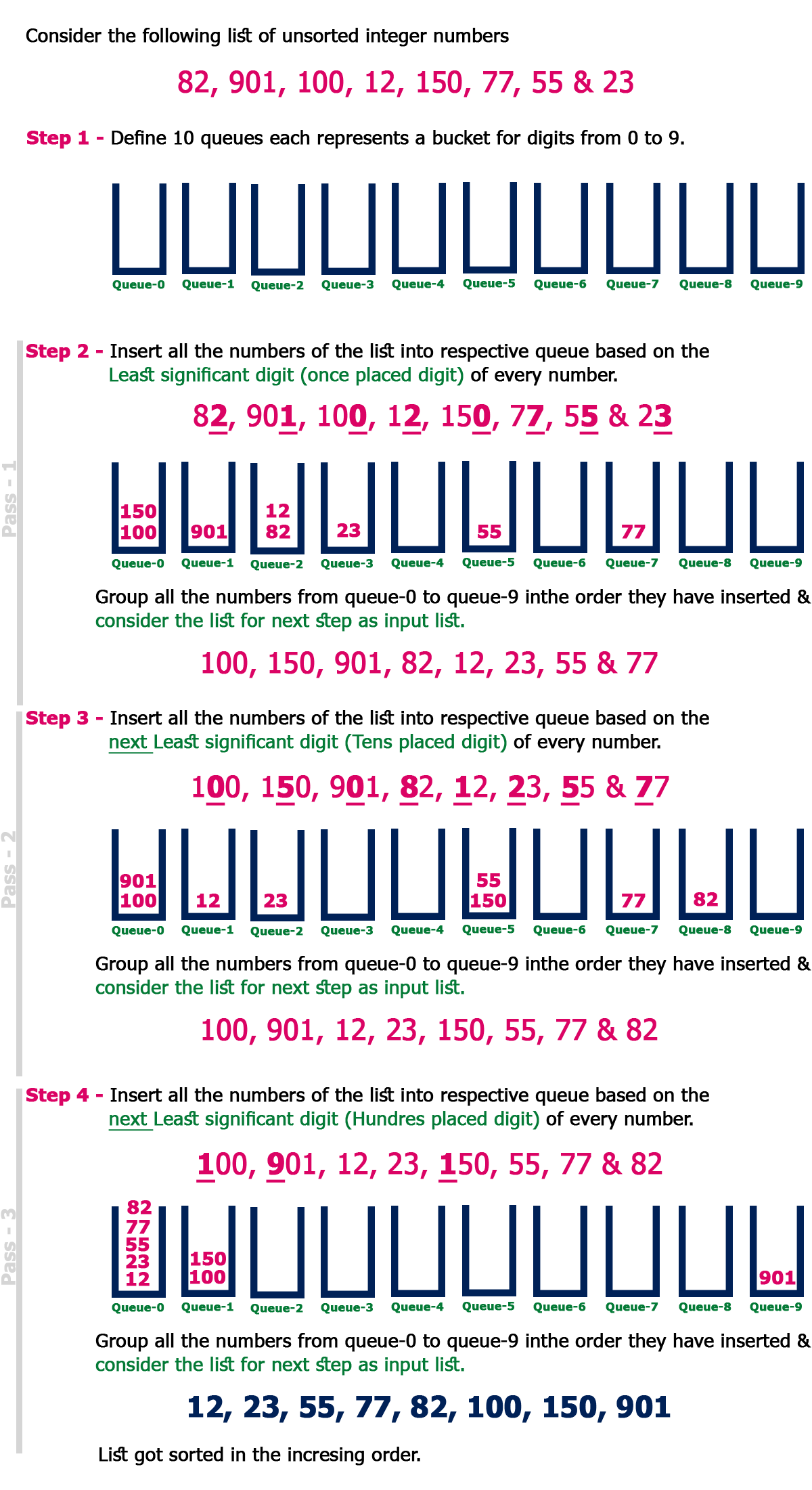
• Step 1 - Define 10 queues each representing a bucket for each digit from 0 to 9.
• Step 2 - Consider the least significant digit of each number in the list which is to be sorted.
• Step 3 - Insert each number into their respective queue based on the least significant digit.
• Step 4 - Group all the numbers from queue 0 to queue 9 in the order they have inserted into their respective queues.
• Step 5 - Repeat from step 3 based on the next least significant digit.
• Step 6 - Repeat from step 2 until all the numbers are grouped based on the most significant digit.

Example

Complexity of the Radix Sort Algorithm

To sort an unsorted list with 'n' number of elements, Radix sort algorithm needs the following complexities...

Worst Case : O(n)
Best Case : O(n)
Average Case : O(n)

#include <stdio.h>
#include <conio.h>
#include <stdlib.h>


int getMax(int list[], int n) {
    int mx = list[0];
    int i;
    for (i = 1; i < n; i++)
        if (list[i] > mx)
            mx = list[i];
    return mx;
}

void countSort(int list[], int n, int exp) {
    int output[n];
    int i, count[10] = { 0 };

    for (i = 0; i < n; i++)
        count[(list[i] / exp) % 10]++;

    for (i = 1; i < 10; i++)
        count[i] += count[i - 1];

    for (i = n - 1; i >= 0; i--) {
        output[count[(list[i] / exp) % 10] - 1] = list[i];
        count[(list[i] / exp) % 10]--;
    }

    for (i = 0; i < n; i++)
        list[i] = output[i];
}

void radixsort(int list[], int n) {
    int m = getMax(list, n);

    int exp;
    for (exp = 1; m / exp > 0; exp *= 10)
        countSort(list, n, exp);
}

void print(int list[], int n) {
    int i;
    for (i = 0; i < n; i++)
        printf("%d\t", list[i]);
}

int main()
{
    int list[] = { 82, 901, 100, 12, 150, 77, 55, 23 };
    int i, n = sizeof(list) / sizeof(list[0]);

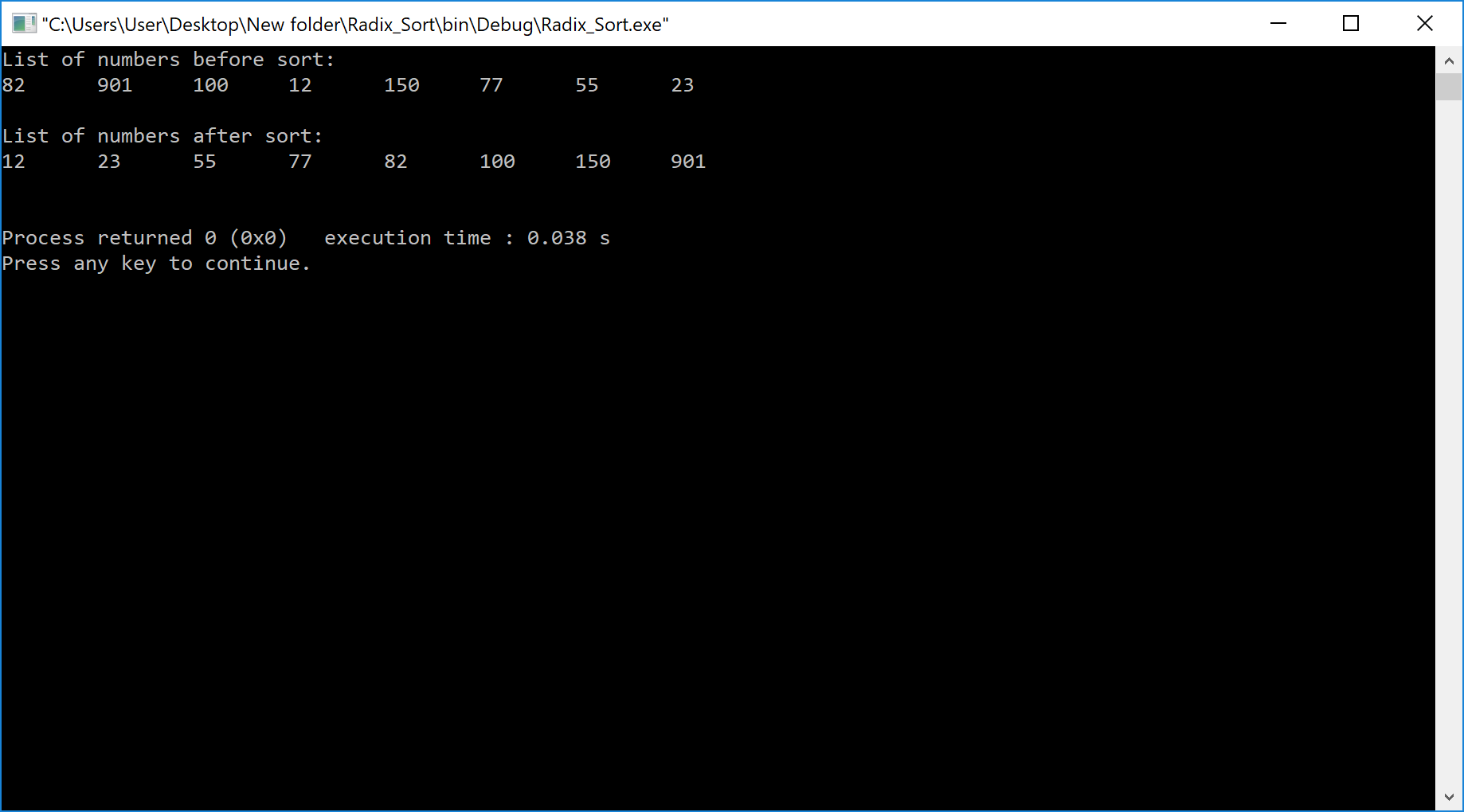
    printf("List of numbers before sort: \n");
    for(i = 0; i<8; i++)
        printf("%d\t", list[i] );

    radixsort(list, n);

    printf("\n\nList of numbers after sort: \n");
    print(list, n);
    printf("\n\n");
    return 0;
}

Output