Insertion Sort Algorithm
Sorting is the process of arranging a list of elements in a particular order (Ascending or Descending).
Insertion sort algorithm arranges a list of elements in a particular order. In insertion sort algorithm, every iteration moves an element from unsorted portion to sorted portion until all the elements are sorted in the list.
Step by Step Process
The insertion sort algorithm is performed using the following steps...
- Step 1 - Assume that first element in the list is in sorted portion and all the remaining elements are in unsorted portion.
- Step 2: Take first element from the unsorted portion and insert that element into the sorted portion in the order specified.
- Step 3: Repeat the above process until all the elements from the unsorted portion are moved into the sorted portion.
Following is the sample code for insertion sort...
Insertion Sort Logic
//Insertion sort logic
for i = 1 to size-1 {
temp = list[i];
j = i-1;
while ((temp < list[j]) && (j > 0)) {
list[j] = list[j-1];
j = j - 1;
}
list[j] = temp;
}
Example

Complexity of the Insertion Sort Algorithm
To sort an unsorted list with 'n' number of elements, we need to make (1+2+3+......+n-1) = (n (n-1))/2 number of comparisions in the worst case. If the list is already sorted then it requires 'n' number of comparisions.
Worst Case : O(n2)
Best Case : Ω(n)
Average Case : Θ(n2)
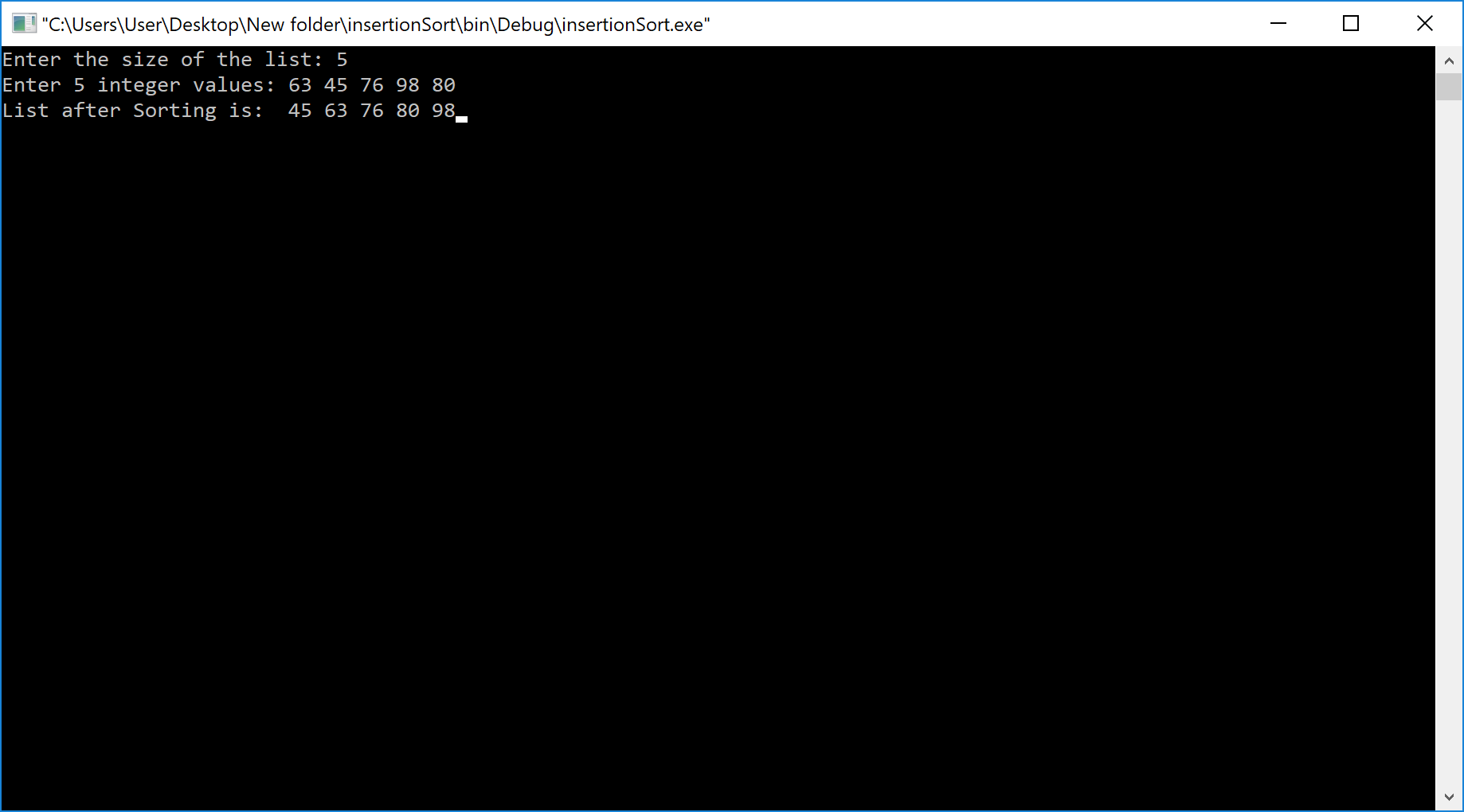
Implementaion of Insertion Sort Algorithm using C Programming Language
#include<stdio.h>
#include<conio.h>
void main(){
int size, i, j, temp, list[100];
printf("Enter the size of the list: ");
scanf("%d", &size);
printf("Enter %d integer values: ", size);
for (i = 0; i < size; i++)
scanf("%d", &list[i]);
//Insertion sort logic
for (i = 1; i < size; i++) {
temp = list[i];
j = i - 1;
while ((temp < list[j]) && (j >= 0)) {
list[j + 1] = list[j];
j = j - 1;
}
list[j + 1] = temp;
}
printf("List after Sorting is: ");
for (i = 0; i < size; i++)
printf(" %d", list[i]);
getch();
}
Output