In search trees like binary search tree, AVL Tree, Red-Black tree, etc., every node contains only one value (key) and a maximum of two children. But there is a special type of search tree called B-Tree in which a node contains more than one value (key) and more than two children. B-Tree was developed in the year 1972 by Bayer and McCreight with the name Height Balanced m-way Search Tree. Later it was named as B-Tree.

B-Tree can be defined as follows...

B-Tree is a self-balanced search tree in which every node contains multiple keys and has more than two children.

Here, the number of keys in a node and number of children for a node depends on the order of B-Tree. Every B-Tree has an order.

B-Tree of Order m has the following properties...

• Property #1 - All leaf nodes must be at same level.
• Property #2 - All nodes except root must have at least [m/2]-1 keys and maximum of m-1 keys.
• Property #3 - All non leaf nodes except root (i.e. all internal nodes) must have at least m/2 children.
• Property #4 - If the root node is a non leaf node, then it must have atleast 2 children.
• Property #5 - A non leaf node with n-1 keys must have n number of children.
• Property #6 - All the key values in a node must be in Ascending Order.

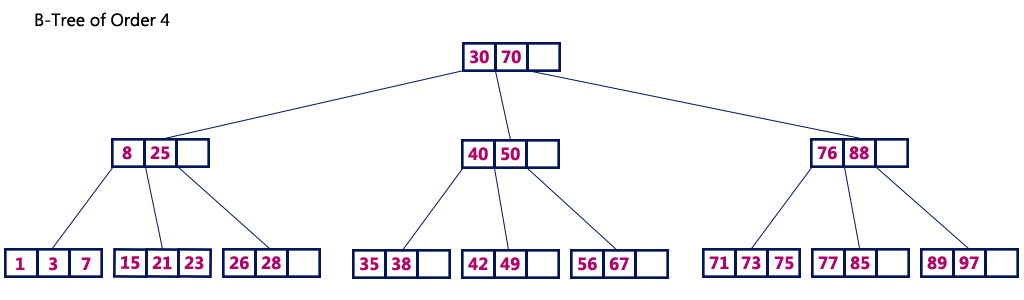
For example, B-Tree of Order 4 contains a maximum of 3 key values in a node and maximum of 4 children for a node.

Example

Operations on a B-Tree

The following operations are performed on a B-Tree...

1. Search
2. Insertion
3. Deletion

Search Operation in B-Tree

The search operation in B-Tree is similar to the search operation in Binary Search Tree. In a Binary search tree, the search process starts from the root node and we make a 2-way decision every time (we go to either left subtree or right subtree). In B-Tree also search process starts from the root node but here we make an n-way decision every time. Where 'n' is the total number of children the node has. In a B-Tree, the search operation is performed with O(log n) time complexity. The search operation is performed as follows...

• Step 1 - Read the search element from the user.
• Step 2 - Compare the search element with first key value of root node in the tree.
• Step 3 - If both are matched, then display "Given node is found!!!" and terminate the function
• Step 4 - If both are not matched, then check whether search element is smaller or larger than that key value.
• Step 5 - If search element is smaller, then continue the search process in left subtree.
• Step 6 - If search element is larger, then compare the search element with next key value in the same node and repeate steps 3, 4, 5 and 6 until we find the exact match or until the search element is compared with last key value in the leaf node.
• Step 7 - If the last key value in the leaf node is also not matched then display "Element is not found" and terminate the function.

Insertion Operation in B-Tree

In a B-Tree, a new element must be added only at the leaf node. That means, the new keyValue is always attached to the leaf node only. The insertion operation is performed as follows...

• Step 1 - Check whether tree is Empty.
• Step 2 - If tree is Empty, then create a new node with new key value and insert it into the tree as a root node.
• Step 3 - If tree is Not Empty, then find the suitable leaf node to which the new key value is added using Binary Search Tree logic.
• Step 4 - If that leaf node has empty position, add the new key value to that leaf node in ascending order of key value within the node.
• Step 5 - If that leaf node is already full, split that leaf node by sending middle value to its parent node. Repeat the same until the sending value is fixed into a node.
• Step 6 - If the spilting is performed at root node then the middle value becomes new root node for the tree and the height of the tree is increased by one.

Example

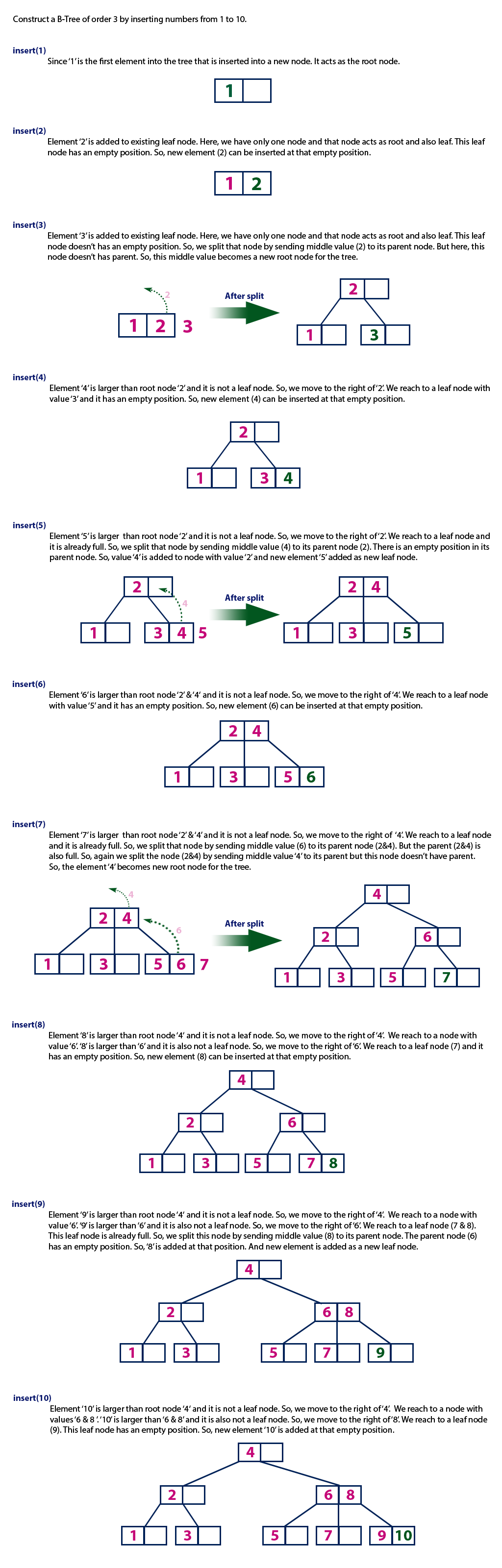
Construct a B-Tree of Order 3 by inserting numbers from 1 to 10.