Graph traversal is a technique used for searching a vertex in a graph. The graph traversal is also used to decide the order of vertices is visited in the search process. A graph traversal finds the edges to be used in the search process without creating loops. That means using graph traversal we visit all the vertices of the graph without getting into looping path.

There are two graph traversal techniques and they are as follows...

1. DFS (Depth First Search)
2. BFS (Breadth First Search)

BFS (Breadth First Search)

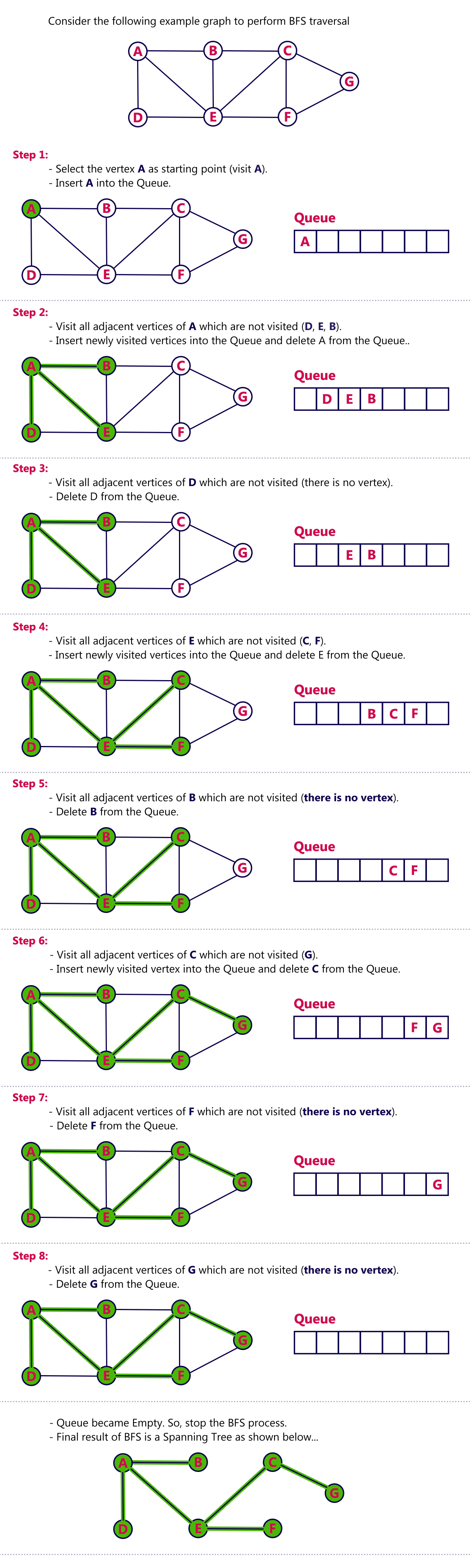
BFS traversal of a graph produces a spanning tree as final result. Spanning Tree is a graph without loops. We use Queue data structure with maximum size of total number of vertices in the graph to implement BFS traversal.

We use the following steps to implement BFS traversal...

• Step 1 - Define a Queue of size total number of vertices in the graph.
• Step 2 - Select any vertex as starting point for traversal. Visit that vertex and insert it into the Queue.
• Step 3 - Visit all the non-visited adjacent vertices of the vertex which is at front of the Queue and insert them into the Queue.
• Step 4 - When there is no new vertex to be visited from the vertex which is at front of the Queue then delete that vertex.
• Step 5 - Repeat steps 3 and 4 until queue becomes empty.
• Step 6 - When queue becomes empty, then produce final spanning tree by removing unused edges from the graph

Example