Introduction to Graphs
Graph is a non-linear data structure. It contains a set of points known as nodes (or vertices) and a set of links known as edges (or Arcs). Here edges are used to connect the vertices. A graph is defined as follows...
Graph is a collection of vertices and arcs in which vertices are connected with arcs
Graph is a collection of nodes and edges in which nodes are connected with edges
Generally, a graph G is represented as G = ( V , E ), where V is set of vertices and E is set of edges.
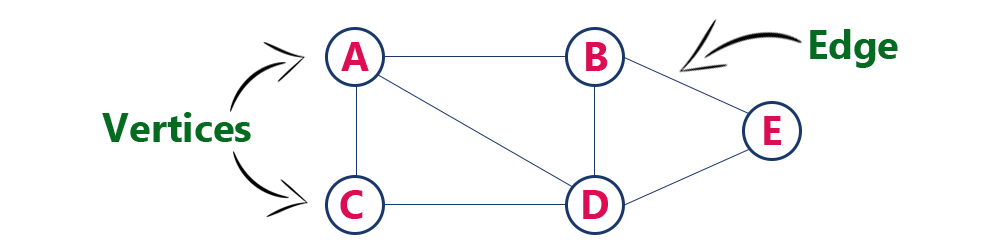
Example
The following is a graph with 5 vertices and 6 edges.
This graph G can be defined as G = ( V , E )
Where V = {A,B,C,D,E} and E = {(A,B),(A,C)(A,D),(B,D),(C,D),(B,E),(E,D)}.
Graph Terminology
We use the following terms in graph data structure...
Vertex
Individual data element of a graph is called as Vertex. Vertex is also known as node. In above example graph, A, B, C, D & E are known as vertices.
Edge
An edge is a connecting link between two vertices. Edge is also known as Arc. An edge is represented as (startingVertex, endingVertex). For example, in above graph the link between vertices A and B is represented as (A,B). In above example graph, there are 7 edges (i.e., (A,B), (A,C), (A,D), (B,D), (B,E), (C,D), (D,E)).
Edges are three types.
- Undirected Edge - An undirected egde is a bidirectional edge. If there is undirected edge between vertices A and B then edge (A , B) is equal to edge (B , A).
- Directed Edge - A directed egde is a unidirectional edge. If there is directed edge between vertices A and B then edge (A , B) is not equal to edge (B , A).
- Weighted Edge - A weighted egde is a edge with value (cost) on it.
Undirected Graph
A graph with only undirected edges is said to be undirected graph.
Directed Graph
A graph with only directed edges is said to be directed graph.
Mixed Graph
A graph with both undirected and directed edges is said to be mixed graph.
End vertices or Endpoints
The two vertices joined by edge are called end vertices (or endpoints) of that edge.
Origin
If a edge is directed, its first endpoint is said to be the origin of it.
Destination
If a edge is directed, its first endpoint is said to be the origin of it and the other endpoint is said to be the destination of that edge.
Adjacent
If there is an edge between vertices A and B then both A and B are said to be adjacent. In other words, vertices A and B are said to be adjacent if there is an edge between them.
Incident
Edge is said to be incident on a vertex if the vertex is one of the endpoints of that edge.
Outgoing Edge
A directed edge is said to be outgoing edge on its origin vertex.
Incoming Edge
A directed edge is said to be incoming edge on its destination vertex.
Degree
Total number of edges connected to a vertex is said to be degree of that vertex.
Indegree
Total number of incoming edges connected to a vertex is said to be indegree of that vertex.
Outdegree
Total number of outgoing edges connected to a vertex is said to be outdegree of that vertex.
Parallel edges or Multiple edges
If there are two undirected edges with same end vertices and two directed edges with same origin and destination, such edges are called parallel edges or multiple edges.
Self-loop
Edge (undirected or directed) is a self-loop if its two endpoints coincide with each other.
Simple Graph
A graph is said to be simple if there are no parallel and self-loop edges.
Path
A path is a sequence of alternate vertices and edges that starts at a vertex and ends at other vertex such that each edge is incident to its predecessor and successor vertex.
