Binary Search Algorithm
What is Search?
Search is a process of finding a value in a list of values. In other words, searching is the process of locating given value position in a list of values.
Binary Search Algorithm
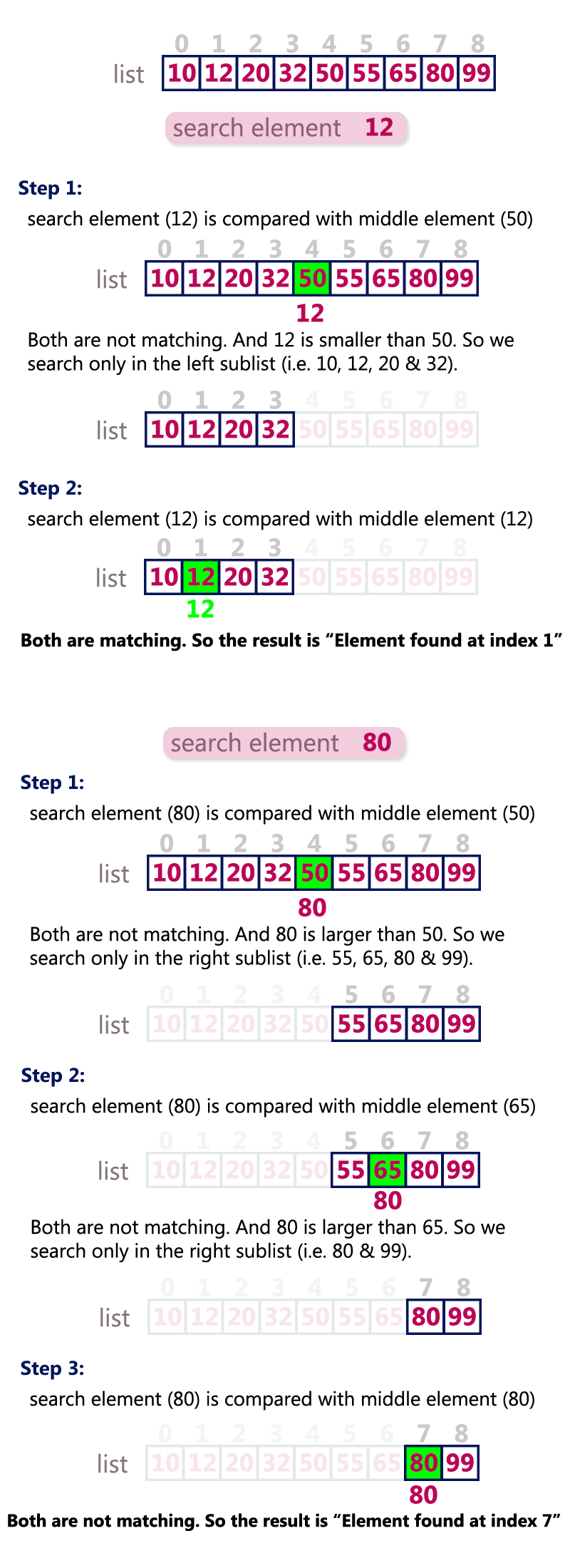
Binary search algorithm finds a given element in a list of elements with O(log n) time complexity where n is total number of elements in the list. The binary search algorithm can be used with only a sorted list of elements. That means the binary search is used only with a list of elements that are already arranged in an order. The binary search can not be used for a list of elements arranged in random order. This search process starts comparing the search element with the middle element in the list. If both are matched, then the result is "element found". Otherwise, we check whether the search element is smaller or larger than the middle element in the list. If the search element is smaller, then we repeat the same process for the left sublist of the middle element. If the search element is larger, then we repeat the same process for the right sublist of the middle element. We repeat this process until we find the search element in the list or until we left with a sublist of only one element. And if that element also doesn't match with the search element, then the result is "Element not found in the list".
Binary search is implemented using following steps...
- Step 1 - Read the search element from the user.
- Step 2 - Find the middle element in the sorted list.
- Step 3 - Compare the search element with the middle element in the sorted list.
- Step 4 - If both are matched, then display "Given element is found!!!" and terminate the function.
- Step 5 - If both are not matched, then check whether the search element is smaller or larger than the middle element.
- Step 6 - If the search element is smaller than middle element, repeat steps 2, 3, 4 and 5 for the left sublist of the middle element.
- Step 7 - If the search element is larger than middle element, repeat steps 2, 3, 4 and 5 for the right sublist of the middle element.
- Step 8 - Repeat the same process until we find the search element in the list or until sublist contains only one element.
- Step 9 - If that element also doesn't match with the search element, then display "Element is not found in the list!!!" and terminate the function.
Example
Consider the following list of elements and the element to be searched...
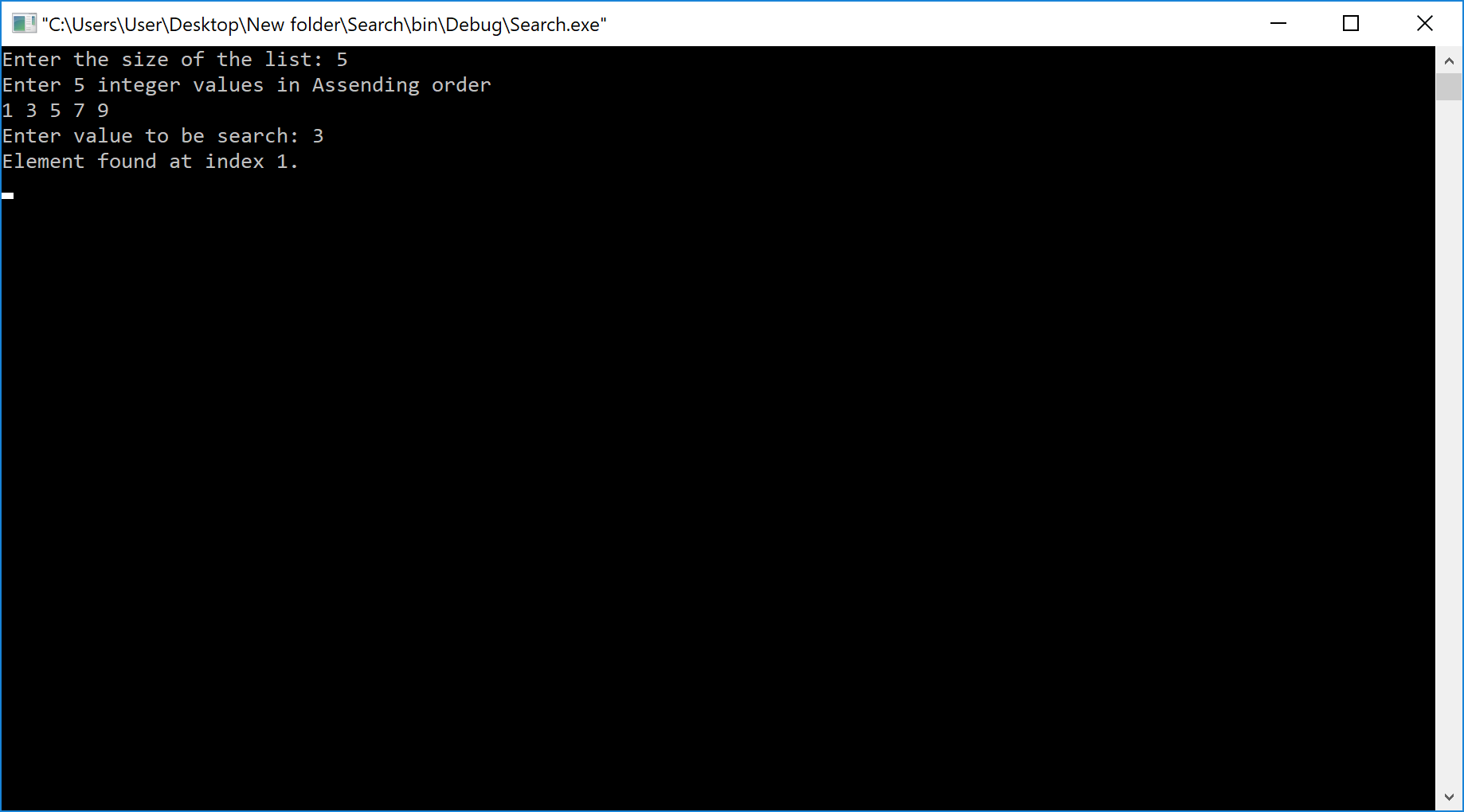
Implementation of Binary Search Algorithm using C Programming Language
#include<stdio.h>
#include<conio.h>
void main()
{
int first, last, middle, size, i, sElement, list[100];
clrscr();
printf("Enter the size of the list: ");
scanf("%d",&size);
printf("Enter %d integer values in Assending order\n", size);
for (i = 0; i < size; i++)
scanf("%d",&list[i]);
printf("Enter value to be search: ");
scanf("%d", &sElement);
first = 0;
last = size - 1;
middle = (first+last)/2;
while (first <= last) {
if (list[middle] < sElement)
first = middle + 1;
else if (list[middle] == sElement) {
printf("Element found at index %d.\n",middle);
break;
}
else
last = middle - 1;
middle = (first + last)/2;
}
if (first > last)
printf("Element Not found in the list.");
getch();
}
Output