AVL Tree Datastructure
AVL tree is a height-balanced binary search tree. That means, an AVL tree is also a binary search tree but it is a balanced tree. A binary tree is said to be balanced if, the difference between the heights of left and right subtrees of every node in the tree is either -1, 0 or +1. In other words, a binary tree is said to be balanced if the height of left and right children of every node differ by either -1, 0 or +1. In an AVL tree, every node maintains an extra information known as balance factor. The AVL tree was introduced in the year 1962 by G.M. Adelson-Velsky and E.M. Landis.
An AVL tree is defined as follows...
An AVL tree is a balanced binary search tree. In an AVL tree, balance factor of every node is either -1, 0 or +1.
Balance factor of a node is the difference between the heights of the left and right subtrees of that node. The balance factor of a node is calculated either height of left subtree - height of right subtree (OR) height of right subtree - height of left subtree. In the following explanation, we calculate as follows...
Balance factor = heightOfLeftSubtree - heightOfRightSubtree
Example of AVL Tree
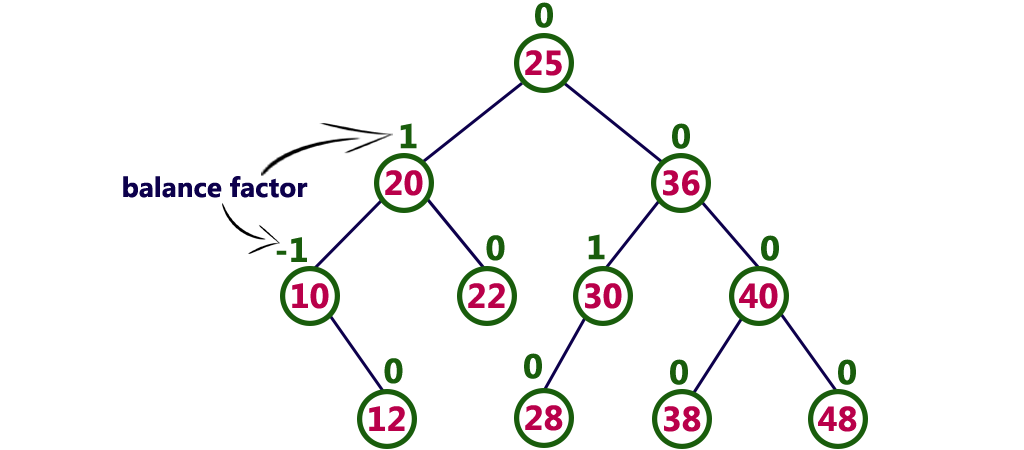
The above tree is a binary search tree and every node is satisfying balance factor condition. So this tree is said to be an AVL tree.
AVL Tree Rotations
In AVL tree, after performing operations like insertion and deletion we need to check the balance factor of every node in the tree. If every node satisfies the balance factor condition then we conclude the operation otherwise we must make it balanced. Whenever the tree becomes imbalanced due to any operation we use rotation operations to make the tree balanced.
Rotation operations are used to make the tree balanced.
Rotation is the process of moving nodes either to left or to right to make the tree balanced.
There are four rotations and they are classified into two types.
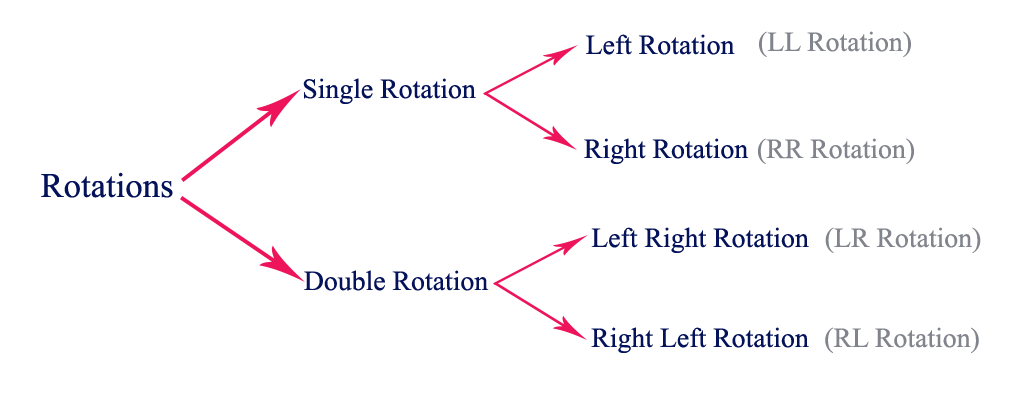
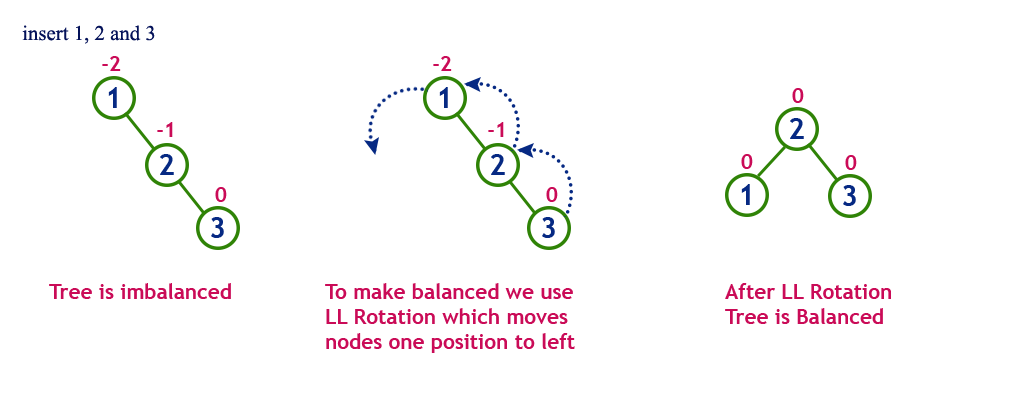
Single Left Rotation (LL Rotation)
In LL Rotation, every node moves one position to left from the current position. To understand LL Rotation, let us consider the following insertion operation in AVL Tree...
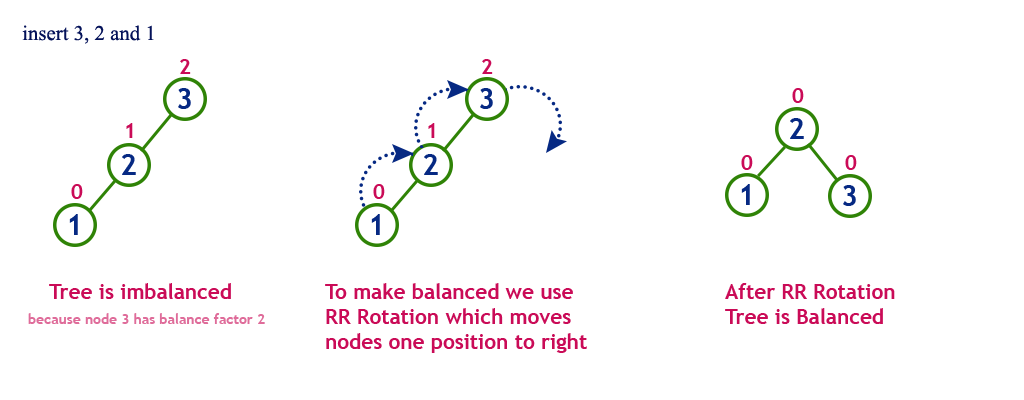
Single Right Rotation (RR Rotation)
In RR Rotation, every node moves one position to right from the current position. To understand RR Rotation, let us consider the following insertion operation in AVL Tree...
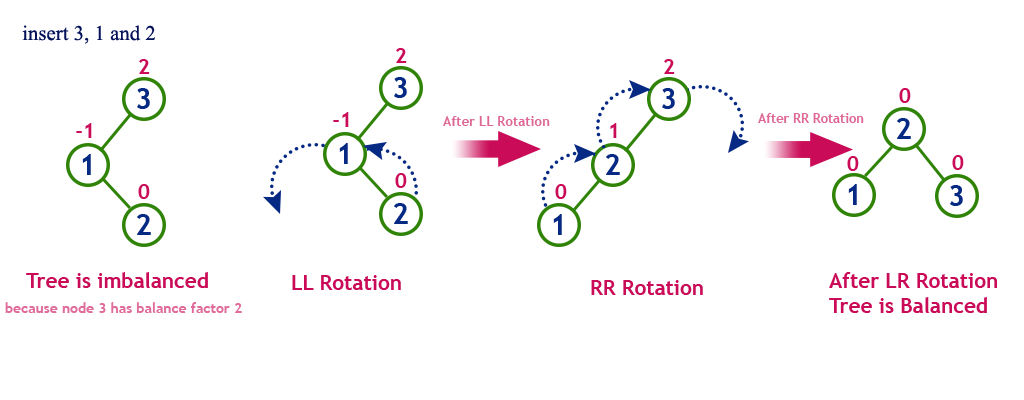
Left Right Rotation (LR Rotation)
The LR Rotation is a sequence of single left rotation followed by a single right rotation. In LR Rotation, at first, every node moves one position to the left and one position to right from the current position. To understand LR Rotation, let us consider the following insertion operation in AVL Tree...
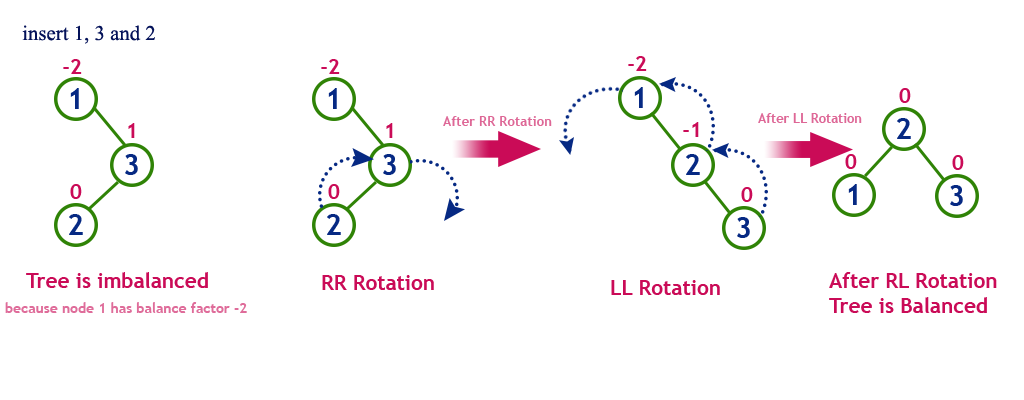
Right Left Rotation (RL Rotation)
The RL Rotation is sequence of single right rotation followed by single left rotation. In RL Rotation, at first every node moves one position to right and one position to left from the current position. To understand RL Rotation, let us consider the following insertion operation in AVL Tree...
Operations on an AVL Tree
The following operations are performed on AVL tree...
- Search
- Insertion
- Deletion
Search Operation in AVL Tree
In an AVL tree, the search operation is performed with O(log n) time complexity. The search operation in the AVL tree is similar to the search operation in a Binary search tree. We use the following steps to search an element in AVL tree...
- Step 1 - Read the search element from the user.
- Step 2 - Compare the search element with the value of root node in the tree.
- Step 3 - If both are matched, then display "Given node is found!!!" and terminate the function
- Step 4 - If both are not matched, then check whether search element is smaller or larger than that node value.
- Step 5 - If search element is smaller, then continue the search process in left subtree.
- Step 6 - If search element is larger, then continue the search process in right subtree.
- Step 7 - Repeat the same until we find the exact element or until the search element is compared with the leaf node.
- Step 8 - If we reach to the node having the value equal to the search value, then display "Element is found" and terminate the function.
- Step 9 - If we reach to the leaf node and if it is also not matched with the search element, then display "Element is not found" and terminate the function.
Insertion Operation in AVL Tree
In an AVL tree, the insertion operation is performed with O(log n) time complexity. In AVL Tree, a new node is always inserted as a leaf node. The insertion operation is performed as follows...
- Step 1 - Insert the new element into the tree using Binary Search Tree insertion logic.
- Step 2 - After insertion, check the Balance Factor of every node.
- Step 3 - If the Balance Factor of every node is 0 or 1 or -1 then go for next operation.
- Step 4 - If the Balance Factor of any node is other than 0 or 1 or -1 then that tree is said to be imbalanced. In this case, perform suitable Rotation to make it balanced and go for next operation.
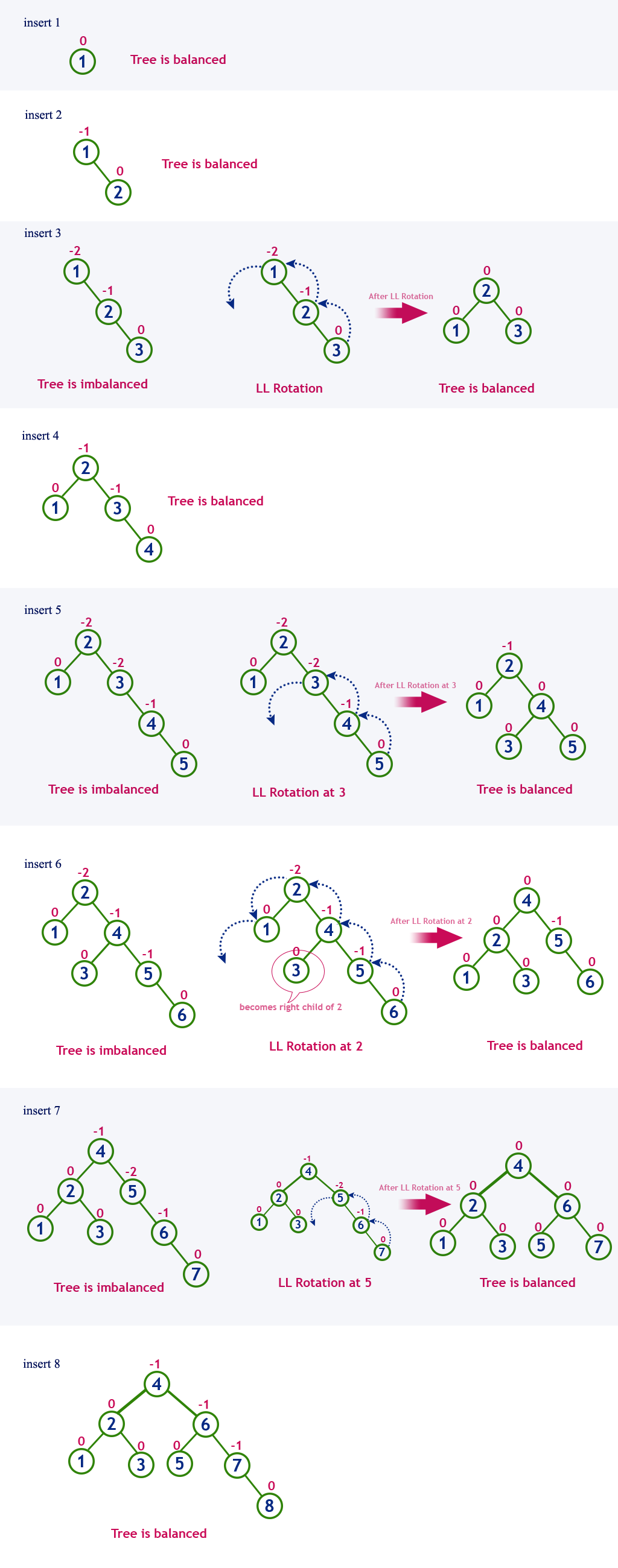
Example: Construct an AVL Tree by inserting numbers from 1 to 8.
Deletion Operation in AVL Tree
The deletion operation in AVL Tree is similar to deletion operation in BST. But after every deletion operation, we need to check with the Balance Factor condition. If the tree is balanced after deletion go for next operation otherwise perform suitable rotation to make the tree Balanced.
