In a binary tree, every node can have a maximum of two children but there is no need to maintain the order of nodes basing on their values. In a binary tree, the elements are arranged in the order they arrive at the tree from top to bottom and left to right.

A binary tree has the following time complexities...

To enhance the performance of binary tree, we use a special type of binary tree known as Binary Search Tree. Binary search tree mainly focuses on the search operation in a binary tree. Binary search tree can be defined as follows...

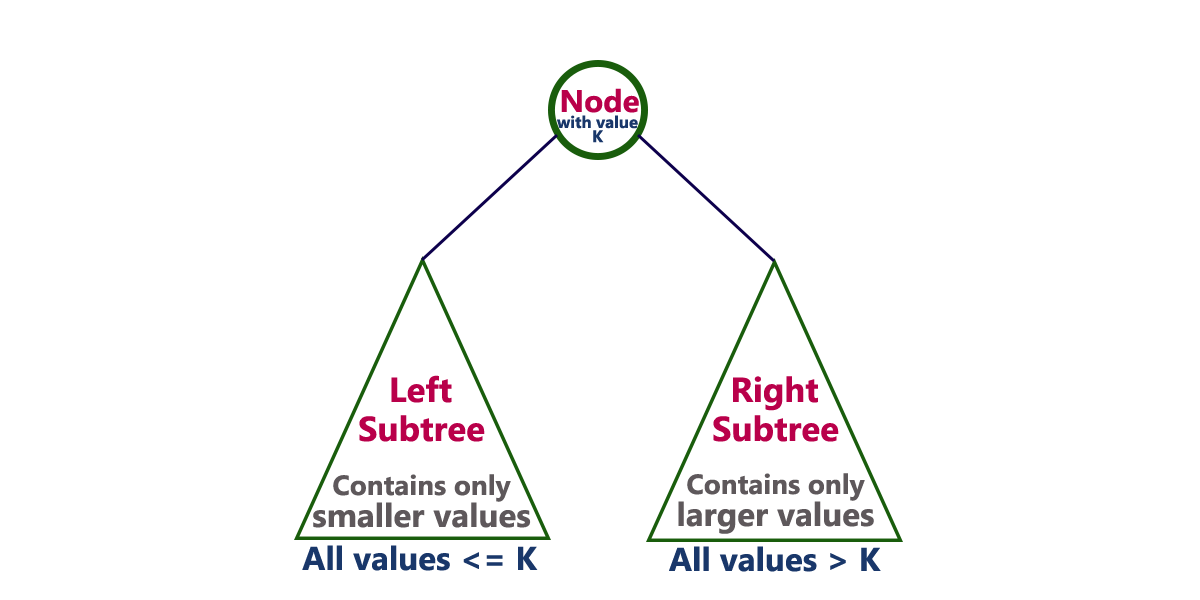
Binary Search Tree is a binary tree in which every node contains only smaller values in its left subtree and only larger values in its right subtree.

In a binary search tree, all the nodes in the left subtree of any node contains smaller values and all the nodes in the right subtree of any node contains larger values as shown in the following figure...

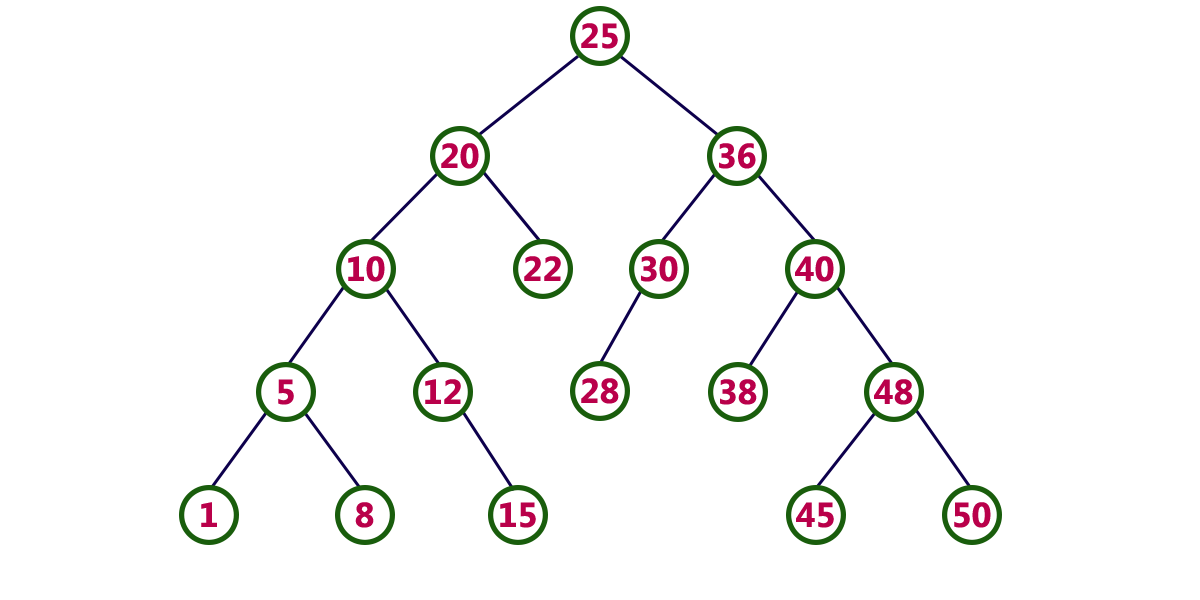
Example

The following tree is a Binary Search Tree. In this tree, left subtree of every node contains nodes with smaller values and right subtree of every node contains larger values.

Operations on a Binary Search Tree

The following operations are performed on a binary search tree...

Search Operation in BST

In a binary search tree, the search operation is performed with O(log n) time complexity. The search operation is performed as follows...

• Step 1 - Read the search element from the user.
• Step 2 - Compare the search element with the value of root node in the tree.
• Step 3 - If both are matched, then display "Given node is found!!!" and terminate the function
• Step 4 - If both are not matched, then check whether search element is smaller or larger than that node value.
• Step 5 - If search element is smaller, then continue the search process in left subtree.
• Step 6- If search element is larger, then continue the search process in right subtree.
• Step 7 - Repeat the same until we find the exact element or until the search element is compared with the leaf node
• Step 8 - If we reach to the node having the value equal to the search value then display "Element is found" and terminate the function.
• Step 9 - If we reach to the leaf node and if it is also not matched with the search element, then display "Element is not found" and terminate the function.

Insertion Operation in BST

In a binary search tree, the insertion operation is performed with O(log n) time complexity. In binary search tree, new node is always inserted as a leaf node. The insertion operation is performed as follows...

• Step 1 - Create a newNode with given value and set its left and right to NULL.
• Step 2 - Check whether tree is Empty.
• Step 3 - If the tree is Empty, then set root to newNode.
• Step 4 - If the tree is Not Empty, then check whether the value of newNode is smaller or larger than the node (here it is root node).
• Step 5 - If newNode is smaller than or equal to the node then move to its left child. If newNode is larger than the node then move to its right child.
• Step 6- Repeat the above steps until we reach to the leaf node (i.e., reaches to NULL).
• Step 7 - After reaching the leaf node, insert the newNode as left child if the newNode is smaller or equal to that leaf node or else insert it as right child.

Deletion Operation in BST

In a binary search tree, the deletion operation is performed with O(log n) time complexity. Deleting a node from Binary search tree includes following three cases...

Case 1: Deleting a leaf node

We use the following steps to delete a leaf node from BST...

• Step 1 - Find the node to be deleted using search operation
• Step 2 - Delete the node using free function (If it is a leaf) and terminate the function.

Case 2: Deleting a node with one child

We use the following steps to delete a node with one child from BST...

• Step 1 - Find the node to be deleted using search operation
• Step 2 - If it has only one child then create a link between its parent node and child node.
• Step 3 - Delete the node using free function and terminate the function.

Case 3: Deleting a node with two children

We use the following steps to delete a node with two children from BST...

• Step 1 - Find the node to be deleted using search operation
• Step 2 - If it has two children, then find the largest node in its left subtree (OR) the smallest node in its right subtree.
• Step 3 - Swap both deleting node and node which is found in the above step.
• Step 4 - Then check whether deleting node came to case 1 or case 2 or else goto step 2
• Step 5 - If it comes to case 1, then delete using case 1 logic.
• Step 6- If it comes to case 2, then delete using case 2 logic.
• Step 7 - Repeat the same process until the node is deleted from the tree.

Example

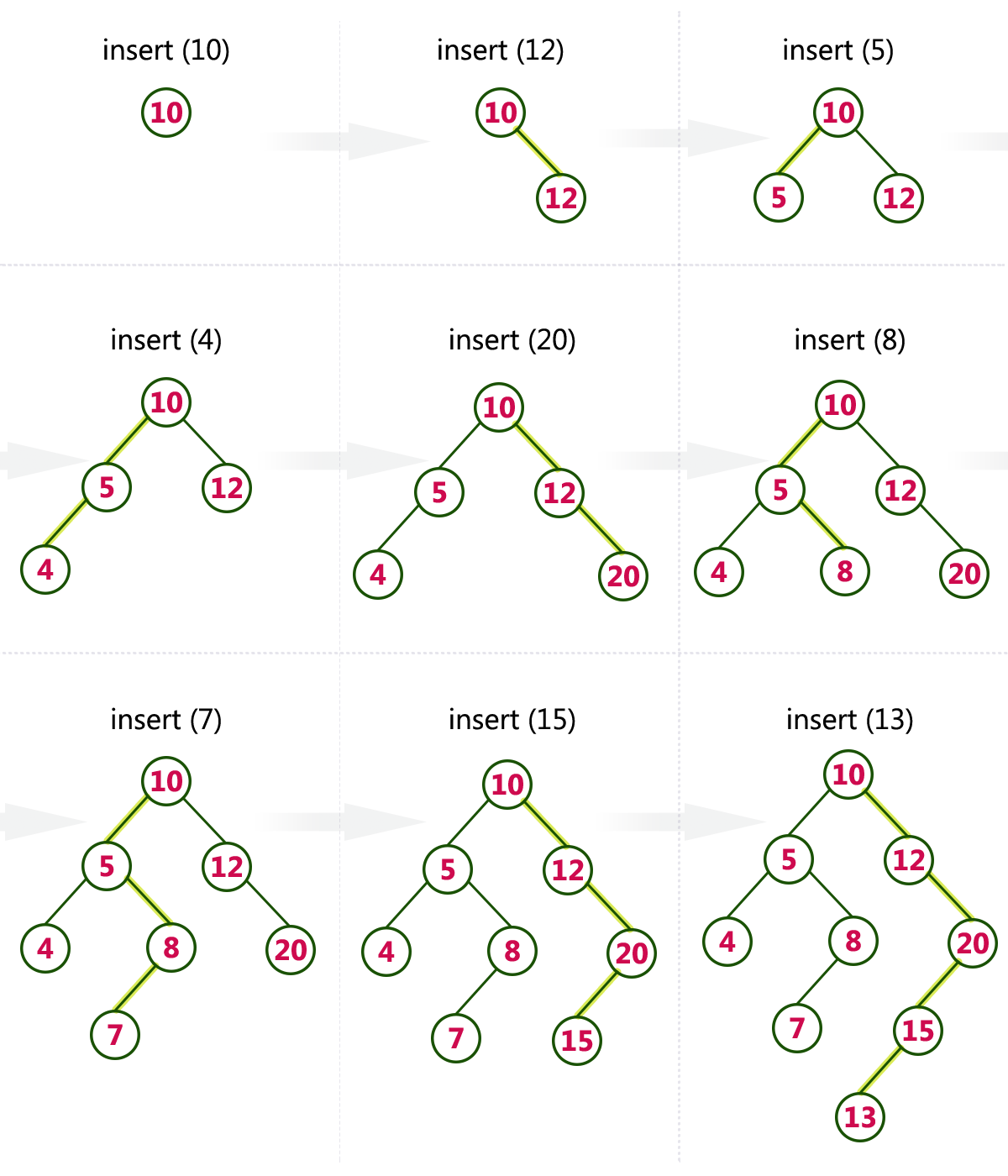
Construct a Binary Search Tree by inserting the following sequence of numbers...

10,12,5,4,20,8,7,15 and 13

Above elements are inserted into a Binary Search Tree as follows...

#include<stdio.h>
#include<conio.h>
#include<stdlib.h>

struct node
{
	int data;
	struct node *left;
	struct node *right;
};


void inorder(struct node *root)
{
	if(root)
	{
		inorder(root->left);
		printf("  %d",root->data);
		inorder(root->right);
	}
}

int main()
{
	int n , i;
	struct node *p , *q , *root;
	printf("Enter the number of nodes to be insert: ");
	scanf("%d",&n);

	printf("\nPlease enter the numbers to be insert: ");

	for(i=0;i<i++)
	{
		p = (struct node*)malloc(sizeof(struct node));
		scanf("%d",&p->data);
		p->left = NULL;
		p->right = NULL;
		if(i == 0)
		{
			root = p; // root always point to the root node
		}
		else
		{
			q = root;   // q is used to traverse the tree
			while(1)
			{
				if(p->data > q->data)
				{
					if(q->right == NULL)
						{
						q->right = p;
						break;
						}
					else
						q = q->right;
				}
				else
				{
					if(q->left == NULL)
						{
						q->left = p;
						break;
						}
					else
						q = q->left;
				}
			}

		}

	}

printf("\nBinary Search Tree nodes in Inorder Traversal: ");
inorder(root);
printf("\n");

return 0;
}

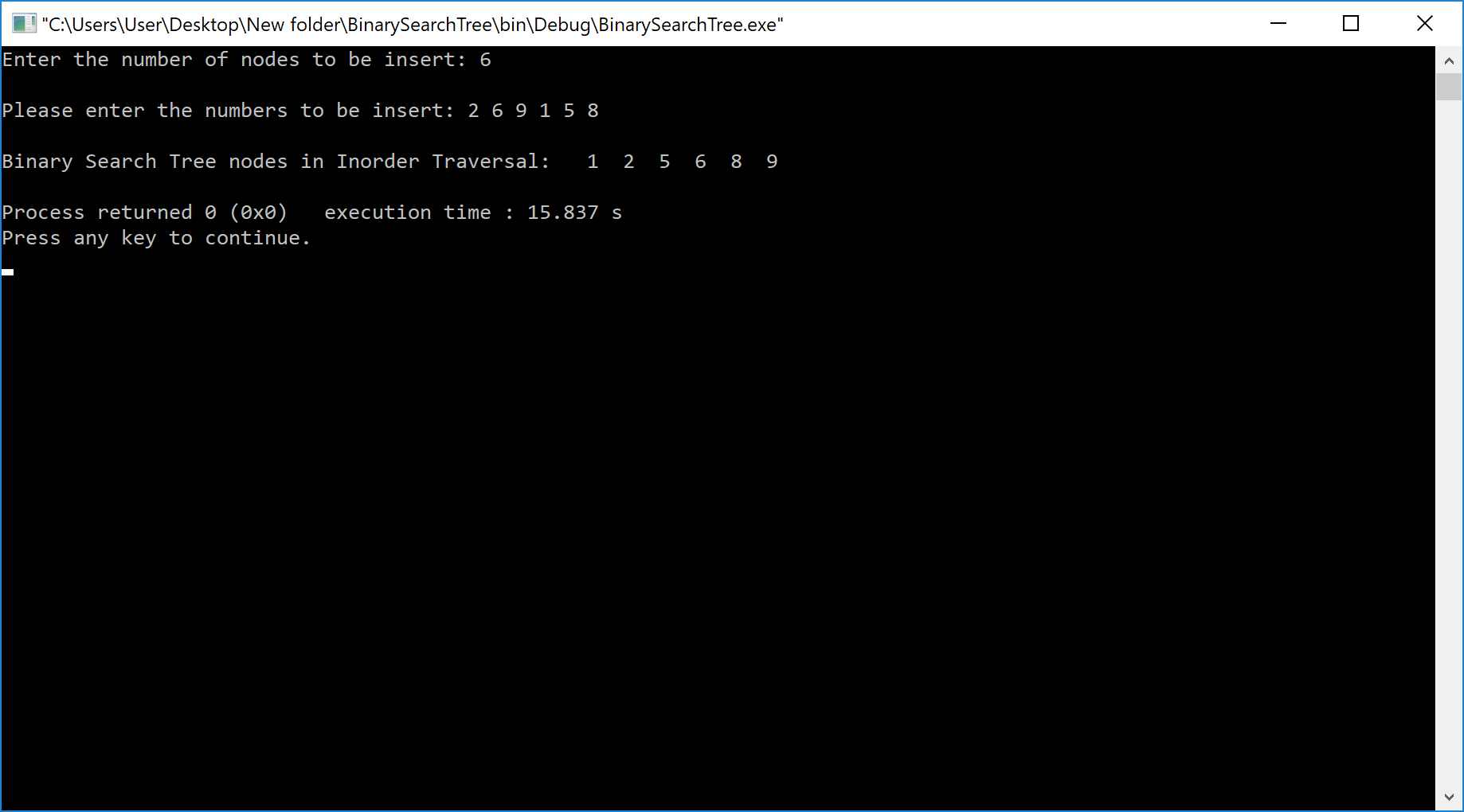
Output